(This is more of an impressions piece. You can find my solution here. Here’s the final result from the methods I used.)
Sunday last week I was doing very little in the afternoon when I decided to watch a recent interview of (Hon. Min.) Sumana Shrestha up on Youtube. It was fairly long (which is sometimes a problem in these attention-deficient times), but I started watching it, and like everything that is interesting, I found myself watching it to the end. She seems seriously to believe in the power of education to change the country. She has my complete support – I have forever been saying education is the answer to all our problems.
Minister Shrestha mentioned in the interview that the education ministry had recently written to Kathmandu University requesting supercomputer priv for a task they had been working on and I remembered the school-matching task she had opened up to the public at the ministry’s (Moest) github. I had first heard about it a week before, but had passed it over. Now I was interested in the problem, because sure I imagine it taking some tricks to “elegantly” solve, but it didn’t need a supercomputer. She might have been referring to some other heavier task for all I know, but I do not imagine we in Nepal really require a supercomputer for our tasks – we might just not have that kind (or amount) of data.
The Problem
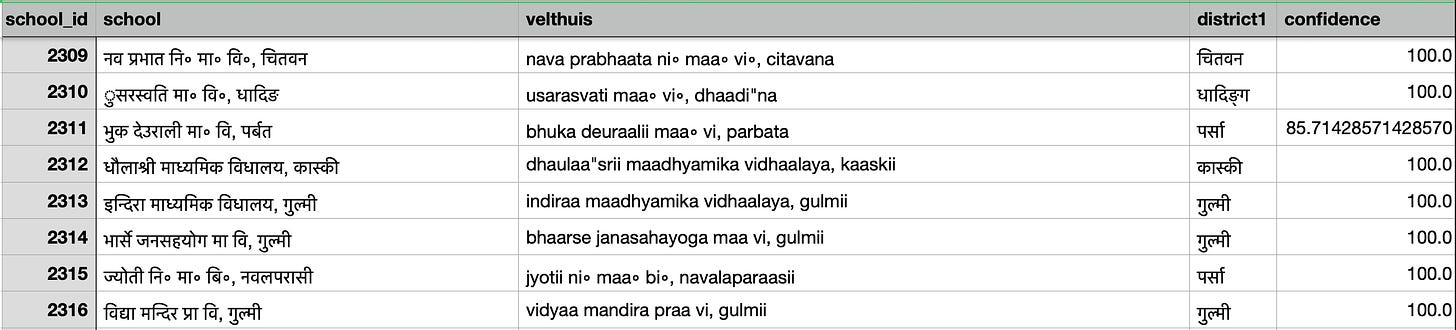
So the task is this: given two lists of schools obtained from two separate sources, one in Nepali another in English, with profuse use of non-standardized shorthand (“Ma V”, “Maa Vi”, “MAVI”, etc. for “Secondary School”; interchangeable use of “Basic School” and “Primary School”) and such other standard noise, find a mapping from the first list to the second. The ideal solution is a 1-1 mapping between the schools.
There are complications even beyond the non-standard naming schemes. Names of schools are very common in Nepal: almost every district has a “Jana Priya” or “Prabhat” or “Bal Sudhar” or “Bal Kalyan”. The district-school matching is not always a 100% correct (see below). You can take a quick peek at the files and you’ll envision even human annotators having trouble matching the schools solely on the basis of their names, maybe even with their districts (two schools with the same name in the same district). This is where we begin.
Solution
A simple and straightforward solution would be to iterate over the names in the first file and for each name try to match it against the names in the second file. That is still polynomial time (k⋅n⋅m where n and m are the number of relevant rows in the first and second files respectively, ~30,000 each, and k is a constant for constant-time operations, assuming those are enough for comparisons), but I’ve seen quotes of one or two computation days for such attempted brute-force approaches in discussions.
When I decided to take a look at the problem, the first thing I did was look up vectorization approaches for similarity matching in strings. (It’s not for nothing that we have linear algebra – you’ve got to use matrices and vectors every chance you get! Period.) Also, like the experts in the field say, TF-IDF always works. N-grams too. It isn’t for nothing that they keep popping up everywhere in NLP.
I found some work in similarity search and one of them pointed me out to this ingenious little library called nmslib (Non-Metric Space Library) which uses both metric and generic non-metric search spaces to perform similarity searching. It’s so quick that even Amazon Elasticsearch uses it. (As I went deeper, I learned that this is not your casual little library the author decided to work on one day because the sun was too hot – it’s a decades-spanning passion and also the topic of one of the author’s PhD at Carnegie Mellon LTI.) But it is quick and focuses on generality (instead of precision and specificity), so it was just the solution I was looking for.
With n-grams and TF-IDF, vectorization and nmslib, the problem was mostly solved to the extent it could be.
First, I cleaned up the data to standardize it. This meant reducing the (lexical) distance (and I use “distance” casually, not as a metric) between the school names as much as possible: use only one way of representing a concept (“Secondary School” instead of all its variants) by regex substitution, translate the Nepali names into English (not the other way around because last I worked on MT, systems still had a harder time going that way). So basically, if the names in both the files (with the help of these lexical transformations) could be made to be as similar as possible, the similarity search algorithm will have an easier time finding matches. I’m now looking into this line of research, so maybe soon I’ll write about that as well.
I have refrained from going into a step-by-step methodology here because I’ve written that in my contribution to the Moest repo. My code is also there if you want to take a look. It is pretty simple and I let nmslib do the heavy lifting for me.
We are using the `negdotprod_sparse_fast` space which, from my early exposure to this subject, I think is a non metric space (please correct me if I’m wrong). The distance function is the negative dot product. The method we are using is `simple_invindx`, which inverts the index to get the mappings.
Two obvious methods I focus on: 1) matching all names in the first list against all names in the second list, or 2) aligning the schools by the district and then matching them. The first method takes a maximum of 200 seconds. (For the second method) Since the school-district mapping in the first file is also not a hundred percent correct, I split the original list A into confidence categories before matching. The second method takes less than 15 seconds. Quick execution times suit tweaking and experimentation well. The quicker it is, the more ideas to try out.
Taking a look at the library’s offerings, there does seem some room for improvement. Using other spaces and methods, comparing metric spaces and non metric spaces on this dataset, preparing a high quality evaluation set - all of these would be great places to look into.
At the end of the day, however, this is not an exact search dataset, so there probably won’t be a perfect 1-1 automatic matching. The goal is to reduce manual work. And with systems that can give you approximate matches with confidence values, you can minimize the manual matching effort by verifying the automatic matches first. And verification is always easier than solving.


hello sir, i hope this message finds you well. loved the article! by any chance had you written an article for the kathmandu post named "from the underground with love". i would love to read it.